Alle Jahre wieder kommt nicht nur das Christuskind, sondern auch das sogenannte Ziegenproblem auf, heuer in der Zeitung „Die Zeit“. Wieder bemühen sich berufene und unberufene Kapazitäten darum, dicke Bücher über das „Problem“ zu schreiben, es gibt über dieses Problem schon einige.
Grundlagen:
Also: In einer amerikanischen Gameshow seit 1963 mit dem Namen "Let's make a Deal" bis in die 90-erJahre stand der Endkandidat, geleitet vom Spielleiter Monty Hall, vor 3 Türen. Hinter diesen Türen waren, für den Kandidaten unsichtbar, nicht aber für den Spielleiter, 2 Ziegen und ein Auto versteckt. Klar ist, nur ein Narr würde sich die Ziegen wünschen. Der Kandidat wählt eine beliebige Tür, daraufhin öffnet der Spielleiter eine ihm bekannte Tür mit einer Ziege und fragt den Kandidaten ob er bei seiner 1. Wahl bleiben oder wechseln wolle. Die US-Mathematikerin Marilyn vos Savant, die den höchsten bis dahin gemessenen IQ von 228 hat (5 Jahre im Guiness Buch der Rekorde), postulierte, dass die Wahrscheinlichkeit bei Wahlwechsel größer sei und wer das nicht verstehe, der habe einen zu niedrigen IQ. Ich habe bislang nicht feststellen können, wie hoch sie die Wahrscheinlichkeit berechnet hat, denn ohne Wechsel ist die Wahrscheinlichkeit für das Auto 1/3. Besonders der 2. Teil des Postulats rief erbitterten Widerstand hervor. Wie konnte das eine Frau wagen! „Selber blöde Ziege“ waren noch die harmlosesten Beleidigungen – nicht in einem Käseblatt, sondern beispielsweise im Spiegel. Wahrscheinlich hatte vos Savant so etwas geahnt oder intendiert. Der Mathematikprofessor Dr. Robert Sachs von der George Mason University schrieb ihr: "Sie haben es vermasselt!" Er war der einzige, der sich bei Marilyn später entschuldigte, als er merkte, dass er von falschen Vorausetzungen ausgegangen war. Lieber später als nie. Eine weiterführende Literatur hierzu sei genannt "Gigerenzer, Risiko, ab Seite 169". Ein Lehrer aus Baden-Würthemberg fühlte sich berufen uns mitzuteilen, dass man solche Probleme dort schon in der 5. Klasse löse! Es wurden sogar Parties veranstaltet, bei denen man mit "Tür"karten das Spiel simulierte, in dem man etwa 100-mal spielte, völlig illusorisch, da ein brauchbares Ergebnis so nie zustande kommt (Gesetz der großen Zahlen, Grenzwert, die Veranstaltungen waren damals wohl ein Vorläufer der TeaParty und man war schon genauso blöd wie heute). Ich habe den Bericht des Spiegel von damals aufgehoben. Ich selbst habe etwa 1994 von dem Problem während einer MNU-Tagung in Marburg in einer Vorlesung gehört
Ich habe damals ein Programm über das Ziegenproblem in PASCAL geschrieben - und hatte es eigentlich im Laufe der Zeit vergessen.
Ich verstehe die Diskussion nicht, die ja seit Jahrzehnten anhält.
Es geht dabei nur um das Problem der Wahrscheinlichkeit bei Wechsel. Unter diesem Aspekt habe ich das „Ziegenproblem“ analysiert und mit 3 Methoden gelöst.
1. Verbal:
Der Kandidat kann doch nur gewinnen, wenn er bei seiner 1. Wahl (was hinter seiner gewählten Tür steht, ist ihm natürlich unbekannt) eine der beiden Ziegen getroffen hat, denn dann sind beide Ziegen (eine war vor dem Wechsel vom Spieler gewählt, die andere hat der Spielleiter geöffnet), weg und es bleibt nur das Auto. Die Wahrscheinlichkeit für eine Ziege bei der 1. Wahl ist 2/3! Das ist auch gleichzeitig die Gesamtwahrscheinlichkeit!
Das heißt aber doch nicht, dass man bei 120 Versuchen (Experimenten) des Wahlwechsels 80-mal das Auto bekommt und 40-mal eine Ziege! Es kann auch 120-mal die Ziege sein. Hier gilt das Gesetz der großen Zahlen! Der Wert 2/3 stabilisiert sich erst bei sehr großer Experimentezahl n, der Grenzwert der Wahrscheinlichkeit P für n gegen Unendlich ist 2/3.
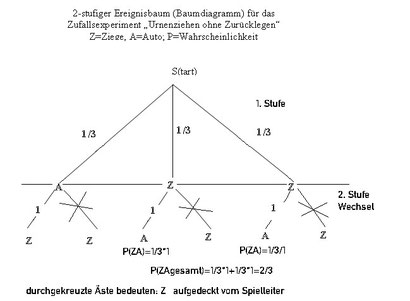
2. Beweisführung mittels Ereignisbaum (s. unten)
Selbstverständlich lässt sich das Problem auch am Baumdiagramm oder Ereignisbaum darstellen:
Mathematisch gesehen handelt es sich um ein zweistufiges Zufallsexperiment ohne Zurücklegen, mit dem Unterschied, dass eine Ziegentür geöffnet wird. Ich will das an einem kleinen Beispiel verdeutlichen:
In einer Urne (Topf, Schachtel, …) liegen 3 Kugeln. 2 ununterscheidbare weiße Kugeln, die den beiden Ziegen entsprechen und eine 1 schwarze Kugel, die dann dem Auto entspricht. Zieht man nun bei der 1 Wahl eine schwarze Kugel (Auto), dann bleibt eine weiße Kugel im Topf, denn die 2. weiße Kugel wurde vom Spielleiter herausgenommen. Es bleibt also für die 2. Wahl nur noch eine weiße Kugel übrig, denn die andere weiße Kugel hat der Spielleiter entfernt. Die einzige schwarze Kugel wurde, für die Spieler unsichtbar, gezogen. Somit befindet sich in der Urne nur noch eine weiße Kugel – also keine schwarze Kugel, stellvertretend für das Auto. Das heißt, wenn der Spieler in seiner 1. Wahl das Auto getroffen hat, kann er nicht mehr gewinnen.
Zieht er aber in seiner 1. Wahl eine der beiden weißen Kugeln, ist diese Kugel nicht mehr im Topf und der Spielleiter entfernt, für den Spieler unreflektiert, die 2. weiße Kugel. Es ist somit nur noch die schwarze Kugel im Topf und die liefert dann sicher dem Spieler das Auto:
(P(auto)=1/3*1+1/3*1=2/3)
Entlang der Zweige werden die Wahrscheinlichkeiten multipliziert und die gesuchten Gewinnereignisse addiert. Die 1 steht dabei für das sichere Ereignis „Auto“ und 1/3 für eine der beiden ununterscheidbaren, gleichberechtigten Ziegen.
3. Programmsimulation:
Den Grenzwert 2/3 zeigt auch mein nachfolgendes, herunterladbares Programm. Dabei habe ich anhand des Ereignisbaumes, der hier wie ein Programmablaufplan (PAP) wirkt, das relativ kurze Programm entwickelt. Ich konnte damit im Kurs „Wahrscheinlichkeitsrechnung“ in der 12. Klasse zeigen, was das Gesetz der großen Zahlen bedeutet, in dem man erst kleine Zahlen eingab und diese ständig erhöhte.
Fazit:Das Ziegenproblem, in der Wissenschaft nach dem Spielleiter als "Monty-Hall-Problem" genannt, lässt sich einem einzigen Satz erklären und lösen:Der Spieler kann bei Wechsel nur dann gewinnen, wenn er in der 1. Wahl eine Ziege hatte, die dann ja mit der vom Spielleiter aufgedeckten Ziege weg ist und es bleibt nur das Auto übrig und die Wahrscheinlichkeit für das Auto ist dann die Anfangswahrscheinlichkeit für eine Ziege, nämlich 2/3.
Allerdings, meine Überlegiungen zur Lösung sind modellhaft, denn Hall hat nicht immer den Wechsel vorgeschlagen, er bot manchmal bis zu 5000 $ für das Nichtwechseln an!
Hier das Turbo-Pascal.Programm:
(läuft nicht unter WIN 10, statt dessen unter Free Pascal)
PROGRAM ziegen;
{Copyright (C) Reinhold Gruninger, Gießen}
USES WINCrt;
VAR i,n,auto:LONGINT;
wahl:BYTE;
wkeit:Real;
BEGIN
RANDOMIZE;
REPEAT
n:=0;wahl:=0;auto:=0;wkeit:=0;
BEGIN
ClrScr;
Writeln('Ziegenproblem: Es gibt 3 Türen, dahinter sind 2 Ziegen und 1 Auto versteckt.');
Writeln('Der Proband wählt eine Tür. Der Spielleiter deckt jetzt eine andere Tür auf,');
Writeln('von der er weiß, dass dort eine Ziege ist. Nun fragt der Spielleiter den Pro-');
Writeln('banden, ob er die Wahl beibehalten will oder die verbleibende Tür wählen will.');
Writeln('Die mathematische Frage ist nun: Ist die Wahrscheinlichkeit größer als bei ');
Writeln('Beibehaltung der ersten Wahl?');
Writeln('Der Spieler gewinnt nur, wenn er als 1. Wahl eine Ziegentür hatte.');
Writeln('Dann gewinnt er aber in jedem Fall!');
Writeln;Writeln;
Write('Wieviel Spiele (es gilt das Gesetz der großen Zahlen!): ');
Readln(n);
FOR i:=1 TO n DO BEGIN {Spieleschleife}
wahl:=RANDOM(3)+1; {Zuweisung}
IF wahl<>1 THEN auto:=auto+1;{1=Auto; 2 und 3 = Ziege}
END; {FOR}
END; {REPEAT}
wkeit:=auto/n*100;
Writeln;Writeln;
Writeln('Die Wahrscheinlichkeit bei ',n,' Durchläufen beträgt ',wkeit:2:2,' %');
Writeln;Writeln;
Writeln('Qualitativ bedeutet dies Ergebnis: Die Gewinnwahrscheinlichkeit ist bei Wechsel größer.');
Writeln('Quantitativ bedeutet das Ergebnis: Die neue Wahrscheinlichkeit ist 2/3,');
Writeln('also doppelt so groß wie die Wahrscheinlichkeit von 1/3 ohne den Wechsel.');
Writeln('Vorausgesetzt mein Programm ist richtig. Auf Schönheit des Textes etc. habe ich verzichtet');
Writeln;Writeln;
Write ('Nochmal (j/n)? ');
UNTIL Readkey='n';
WriteLn;
Write ('Ende');
END.
In großer Trauer und Bestürzung habe ich vernommen, dass mein guter Freund und Berater Professor em. Dr. Oskar Hoffmann am 31.10.2014 nach langer Krankheit verstorben ist.
Wir werden sein Andenken in Ehren halten als einen guten Menschen und guter Lehrer!
Er hat uns immer geholfen, wenn wir Informatiklehrer für unsere Bundeswehrfachschule Gießen benötigten.
PROGRAM minimale_Information_allgemein;
USES WINCrt;
VAR h,z: Byte;
x,a,b,c,y: Real;
BEGIN
REPEAT
ClrScr;
h:=0;
Writeln ('Dieses Programm löst folgende Aufgabe:');
Writeln ('Es sollen 100 Tiere für insgesamt 100 Eu gekauft werden und zwar 3 Tierarten');
Writeln ('Die Lösung kann nur natürliche Zahlen enthalten');
Writeln;writeln;
Write('Gib den Preis für das billigste Tier ein: ');Read(a);Writeln;
Write('Gib den Preis für das mittlere Tier ein : ');Read(b);Writeln;
Write('Gib den Preis für das teuerste Tier ein : ');Read(c);Writeln;
Writeln('Hühner zu ',a:2:1,' Eu, Hasen zu ',b:2:1,' Eu und Rehe zu ',c:2:1,' EU für insgesamt genau 100 Eu');
FOR z:=1 to 100 DO
BEGIN
y:=abs(int((-100/a+c/a*z+100-z)/(1-b/a)));
x:=100-y-z;
IF (x+y+z=100) and (a*x+b*y+c*z=100) and (x<>0) and (x>0) and (y>0) and (z>0)
then begin
h:=h+1;
Writeln ('Die Lösung:',' Hühner: ',x:1:0,' Hasen: ',y:2:0,' Rehe: ',z:1,' Gesamtzahl: ',(x+y+z):0:0);
Writeln ('Gesamtbetrag: ',(a*x+b*y+c*z):2:0,' Euro');
end;
end;
Writeln;Writeln ('Es gibt ',h,' Lösung(en)');
Writeln;Writeln;
Write('Nochmal (j/n)? ');
UNTIL Readkey='n';
END.
